网络科学导论（四）

发表于

4 度相关性与社团结构

4.1 引言

度分布并不能唯一的刻画一个网络，因为具有相同度分布的两个网络可能具有风场不同的其他性质或行为。为了进一步刻画网络的拓扑结构我们需要考虑更多结构信息的高阶拓扑性质。本章介绍刻画网络的二阶度分布特性（也称度相关性）几种不同的方法。

即使是联合概率分布也仍然不能完全刻画网络拓扑。一个典型例子就是复杂网络的社团结构：实际网络往往可以看作是由几个社团组成，社团内部的联系较为紧密，而社团间的联系却比较松散。

4.2 度相关性和同配性

4.2.1 高阶度分布的引入

平均度<k>=2M/N可以看作是网络的0阶度分布特性，他除了告诉我们有多少条边之外并没有告诉我们这些边在网络中的任何信息。

网络的度分布P(k)=n(k)/N可以看作是网络的1阶度分布特征<k>=$\sum_{k=0}^\infty{k}P(k)$，具有相同度分布的两个网络有可能具有非常不同的其他性质或是行为。

4.2.2 联合概率分布

联合概率P(j,k)定义为网络中随机选取的一条边的两个端点的度为j和i的概率，即为网络中度为j和度为i的节点之间存在边占网络中总边数的比例：

$P(i,j)=\frac{m(j,k)\mu{(j,k)}}{2M}$

其中，m(i,j)是度为i和度为j的节点之间的边数；如果i=j那么$\mu(i,j)=2$否则为1

联合概率分布具有如下特征

  1. 记
    $p_k\triangleq{P(k)} \qquad q_k\triangleq{P_n(k)}\qquad e_ {jk}\triangleq{P(j,k)}$
    下式表明网络的2阶度分布特性包含了1阶度分布特性：
    $p_k=\frac{<k>}{k}\sum_{j=k_{min}}^{k_{min}}e_{jk}=\frac{<k>}{k}q_k$

如果网络中两个节点之间是否有边相连与这两个节点的度值无关，也就是说，网络中随机选择的一条边的两个端点的度是完全随机，即有

$e_{jk}=q_jq_k$

那么就称网络不具有度相关性，或着称网络是中性的；否则，就称网络具有度相关性

对于度相关的网络，如果总体上度大的节点倾向于连接度大的节点，那我们就说网络的度是正相关的，这个网络是同配的（Assortative）;如果度大的节点倾向于连接度小的节点，那么我们就称网络的度是负相关的，这个网络是异配的（Disassortative）。具有相同度分布的网络有可能具有完全不同的度相关性。

4.2.3 余平均度

条件概率$P_c(j|k)$定义为在网络中随机选取的一个度为k的节点的邻居节点度为j的概率，它与联合概率P(j,k)有如下的关系：

$P_c(j|k)*P_n(k)=P(j,k)$（4-9）

因此，在给定度分布的情形，条件概率与联合概率可通过式(4-9)得到，如果条件概率$P_c(j|k)$和k相关，就说明节点度之间具有相关性，并且网络拓扑可能具有层次性，如果条件概率$P_c(j,k)$和k没有相关性，那么就说明网络度节点间没有相关性。考虑到任一条边与某个节点相连的概率与该节点的度呈正比，度不相关的网络的条件概率为

$P_n(k'|k)=P_n(k')=\frac{k'P(k')}{<k>}$

另一种更为简洁的判断度相关性的方法是计算度为k的节点的邻居节点的平均度，也称为度为k的节点的余平均度(Excess average degree)，记为<$k_{nn}>(k)$。

设节点i的$k_i$个邻居节点的度为$k_{i_j}$，j=1，2，3…kj我们可以计算节点i的余平均度，即节点i的$k_i$个邻居节点的平均度 如下：

$<k_{nn}>_i=\frac1{k_i}\sum_{j=1}^{k_{i_j}}k_{i_j}$

假设网络中度为k的节点为v1,v2,v3…,那么度为k的节点的余平均度计算如下：

$<k_{nn}>(k)=\frac1{i_k}\sum^{i_k}_{i=1}<k_{nn}>_{v_i}$

$<k_{nn}>(k)$与条件概率和联合概率之间具有如下关系

$<k_{nn}>(k)=\sum^{k_{max}}_{k'=k_{min}}k'P_c(k'|k)=\frac1{q_k}\sum_{k'=k_{min}}^{k_{max}}k'e_{kk'}$ (4-13)

如果$<k_{nn}>(k)$是k的增函数，那么意味着平均而言度大的节点倾向于连接度大的节点，从而表明是同配的；反之则是异配的；如果两者无关，则表明网络中不具有度相关性：

$<k_{nn}>(k)=\frac{\sum_jje_{jk}}{\sum_{j}e_{jk}}=\frac{\sum_jjq_jq_k}{q_k}=\sum_jjq_j=\sum_jj\frac{jp_j}{<k>}=\frac{<k^2>}{<k>}$ (4-14)

与联合概率分布矩阵$(e_{jk})_{k_{max}*k_{max}}$相比，余平均度更为直观但不易于比较不同规模的网络。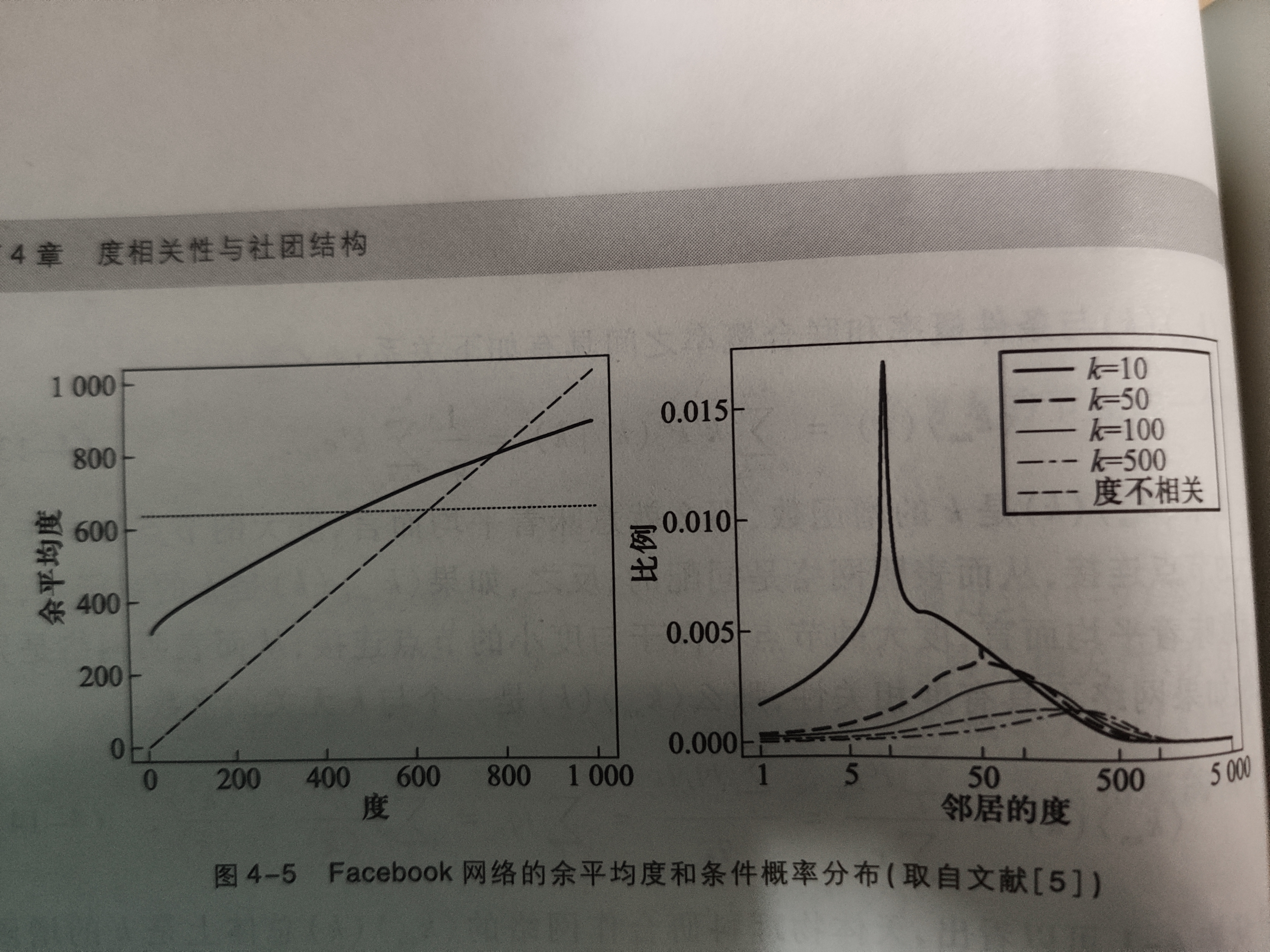
Alt text

上图为例，FaceBook的用户节点的余平均度随着k的增加而增加，可知facebook的用户网络是同配的。作为对比，4-5中的水平虚线是指在假设假设网络不具有度相关性时的期望余平均度<k2>/<k>=635。另外一个值得关注的点时途中实线和虚线的交点在k=700附近，意味着大体上来讲除非你的朋友数大于700，否则你的朋友比你拥有更多的朋友的概率很大，而在facebook中92%的用户的朋友数都远低于这个值

上图的第二幅图表明时k=10，50，100，500时的facebook网络的条件概率$P_c(j|k)$其中纵坐标是线性坐标，横坐标是对数坐标。随着k的增加，曲线的峰值也逐渐向右靠拢，表明度大的节点个更为倾向于连接度大的节点，从而表明网络是同配的，此外除了k=500的情形，其余的图像的都显示条件概率分布的均值都明显大于假设网络不具有度相关性时的期望条件概率分布的均值$k’P(k’)/<k>$

4.2.4 同配系数

网络是度县官的就意味着$e_{jk}$与$q_jq_k$之间不恒等。可以考虑采用两者之间的差的大小来刻画网络的同配或者异配程度，即如下定义度的相关函数

$<jk>-<j><k>=\sum_{j,k}jk(e_{jk}-q_jq_k)$（4-15）

一般而言，规模大的网络根据式4-15计算得到的值的绝对值也大，但可以通过归一化解决这个问题，从而比较不同网络环境中同配或异配程度。当网络为完全同配时，$e_{jk}=q_k\delta_{jk}$式4-15达到最大值，即为余度分布$q_k$的方差

$\sigma_q^2=\sum{k^2}q_k^2-[\sum_kkq_k]^2$(4-16)

于是得到归一化的相关系数，也称为同配系数

$\frac1{\sigma_q^2}\sum_{j,k}jk(e_{jk}-q_jq_k)$(4-17)

显然$r\in[-1,1]$。如果r>,那么网络是同配的；如果r<0那么网络是异配的。|r|的大小反映了同配或者异配系数的强弱程度，同配和异配对网络的鲁棒性和传播性有显著的影响。

4.2.5 实际网络的同配性质

蛋白质交互网络，神经网络等生物网络以及www等技术网络都是异配的，包括科研人员合作和电影演员合作在内的许多现实社会网络往往具有较为明显的同配特性，而不同的在线社会网络却可能呈现不同的同配、异配或接近中性的特征。例如包含1亿个节点的韩国社交网站Cyworld具有异配特征r=-0.13，而facebook则具有同配特征r=0.226.

关于现实社会中的网络的同配性有很多种解释，普通人通常都期望和比自己优秀的人建立联系，而精英也倾向于和精英建立联系，此外，现实网络的同配性也可能和网络属于从属网络（二分网络）有关。

4.2.6 同配概念的一般化

同配概念的一般化理解就是，相似的节点更加倾向于相互连接。
关于社会网络的同质性有两个解释，第一种是选择，即和相似的人称为朋友；第二种是影响，人们由于成为朋友而变得更加相似。社会网络分析的难点之一在于如何区分这两者的效果。难点在于，一方面我们需要知晓网络的拓扑随着时间演化的规；另一方面我们需要对结构和个体行为的联合演化建立合适的模型

度的同配系数可以推广到其他属性的情形。我们用标量参数$x_i$表示节点i的某个属性。假设一个无向网络中有M条边，$A=(a_{ij})$为网络的邻接矩阵。每条边有两个端点，对所有M条边的2M个端点的属性值取平均：

$\mu=\frac{\sum_{i,j}a_{ij}x_i}{\sum_{i,j}a_{ij}}=\frac{\sum_ik_ix_i}{\sum_ik_i}=\frac1{2M}\sum_ik_ix_i$ (4-18)

由于度为$k_i$的一个节点是$k_i$条边的端点，因而在上式的最后一个求和中含有因子ki

考虑网络中每条边的两个端点i和j所对应的$(x_i,x_j)$，它们对于所有的边的协方差为

$\begin{equation}cov(x_i,x_j)=\frac{\sum_{i,j}a_{ij}(x_i-\mu)(x_j-\mu)}{\sum_{i,j}a_{ij}}\\=\frac1{2M}\sum_{i,j}a_{ij}(x_ix_j-\mu{x_i }-\mu{x_j}+\mu^2)\\ =\frac1{2M}\sum_{i,j}a_{ij}x_ix_j-\mu^2\\=\frac1{2M}\sum_{i,j}a_{ij}x_ix_j-\frac{1}{2M^2}\sum_{i,j}k_ik_jx_ix_j\\=\frac1{2M}\sum_{i,j}(a_{ij}-\frac{k_ik_j}{2M})x_ix_j\end{equation}$
令$x_i=x_j$得到$x_i$的方差如下：
$\begin{equation}\sigma_x^2=\frac1{2M}\sum_{i,j}(a_{ij}-\frac{k_ik_j}{2M})x_i^2\\=\frac1{2M}\sum_{i,j}(k_i\delta_{ij}-\frac{k_ik_j}{2M})x_ix_j\end{equation}$
**同配系数**就定义为归一化的协方差，即如下的Pearson相关系数：
$r=\frac{ucov(x_i,x_j)}{\sigma_x^2}=\frac{\sum_{i,j}(a_{ij}-\frac{k_ik_j}{2M})x_ix_j}{\sum_{i,j}(k_i\delta_{ij}-\frac{k_ik_j}{2M})x_ix_j}$(4-20)
如果属性值$x_i$就是度值$k_i$，那么同配系数为
$r=\frac{\sum_{i,j}(a_ij-\frac{k_ik_j}{2M})k_ik_j}{\sum{i,j}(k_i\delta_{ij}-\frac{k_ik_j}{2M})k_ik_j}$(4-21)
上式可进一步表达为
$r=\frac{S_1S_e-S_2^2}{S_1S_3-S_2^2}$(4-22)
其中，
$S_e=\sum_{i,j}a_{ij}k_ik_j=2\sum_{(i,j)\in{E}}k_ik_j, S_1=\sum_ik_i S_2=\sum_ik_i^2,S_3=\sum_ik_i^3$

4.3 社团结构与模块度

4.3.1 社团结构的描述

社团结构分析问题和计算机中的图分割和社会学中的分级聚类等有着密切的关系。社团分割算法整体分为两类，凝聚算法（Agglomerative method）和分裂算法（Divsive method）

4.3.2 模块度

模块度（Modularity）是近年常用的一种衡量社团划分质量的标准，其基本思想是在划分后与相应的零模型（Null Model），以度量划分的质量。网络的零模型，就是指与该网络具有某些相同的性质（如相同的边或者相同的度分布）而在其他方面完全随机的随机图模型。零模型在社团结构研究中需要仔细考量，最低阶的零模型是与原网络具有相同边数的ER随机图模型，它具有均匀度分布，所以目前分析网络社团结构时，通常是把待研究的网络与具有相同度序列的随机图也称为一阶零模型作比较。

对于一个给定的实际网络，假设找到了一种社团划分，那么所有社团内部的边数的总和可计算如下：

$Q_{real}=\frac12\sum_{ij}a_{ij}\delta(C_i,C_j)$

其中A=$(a_{ij})$是实际网络的邻接矩阵，$C_i$与$C _j$分别表示节点i与节点在网络中所属的社团：如果这两个节点属于同一个社团，$\delta$为1否则为0。

对于与该实际网络对应的一个相同规模的零模型，如果用相同的社团划分，那么所有社团内部的边数总和的期望值为

$Q_{null}=\frac12\sum_{ij}p_{ij}\delta(C_i,C_j)$

其中$p_{ij}$是零模型中节点i和节点j之间连边数的期望值。

一个网络的模块度定义为该网络的社团内部边数与相应的零模型内部边数之差占整个网络边数M的比例即

$Q=\frac{Q_{real}-Q_{null}}{M}=\frac1{2M}\sum_{ij}(a_{ij}-p_{ij})\delta(C_i,C_j)$(4-23)

在理论上，对于原网络具有相同度序列但不具有相同度相关性的一个常用的零模型——-配置模型，我们有$p_{ij}=\frac{k_ik_j}{2M}$，这里$k_i$和$k_j$分别为原网络中节点i和节点j的度。因此，常用的模块度定义为

$Q=\frac{1}{2M}\sum_{ij}(a_{ij}-\frac{k_ik_j}{2M})\delta(C_i,C_j)=\frac1{2M}\sum_{ij}b_{ij}\delta(C_i,C_j)$(4-24)
其中
$b_{ij}=a_{ij}-\frac{k_ik_j}{2M}$(4-25)
**B**=$(b_{ij})_{N*N}$也称为**模块度矩阵**(Modularity matrix) 实际网络数据通常包含的是节点间的连边信息，而不会直接给出各个点的度值。为此，下面给出模块度的一种更便于实际计算的形式。 记$e_{vw}$为社团v和社团w之间的连边占整个网络边数的比例，有
$e_{vw}=\frac1{2M}\sum_{ij}a_{ij}\delta(C_i,v)\delta(C_j,w)$

记$a_v$为一端与社团v中节点相连的连边的比例，则有

$a_v=\frac1{2M}\sum_{i}k_i\delta(C_i,v)$
于是[式(4-24)](#_4_24)可以写为
$\begin{equation}Q=\frac1{2M}\sum_{ij}(a_{ij}-\frac{k_ik_j}{2M})\sum_v\delta(C_i,v)\delta(C_j,v) \\ =\sum_v[\frac1{2M}\sum_{ij}a_{ij}\delta(C_i,v)\delta(C_j,v)-\frac1{2M}\sum_ik_i\delta(C_i,v)\frac1{2M}\sum_jk_j\delta(C_j,v)]\\=\sum_v[e_{vv}-a_v^2]\end{equation}$

式4-25意味着，只要跟就网络连边数统计出每个社团v内部节点之间的连边数占整个网络边数的比例$e_{vv}$，以及一端与社团v中节点相连的连边的比例$a_v$，就可计算出模块度。$a_v^2$还有一个清晰的物理意义：它表示的是在相应的具有相同度序列的配置模型中这些节点之间的连边数占整个网络边数比例的期望值。因此，式4-25的另一种等价表达方式为：

$Q=\sum_{v=1}^{n_e}[\frac{l_v}{M}-{(\frac{d_v}{2M})}^2]$(4-26)
其中$n_c$是社团的数量，$l_v$是社团v内部所包含的边数，$d_v$是社团v中所有节点的度值之和。 给定一个网络，不同的社团分割所对应的模块度值一般也是不同的。极端情况是所有节点都属于一个社团，那么模块度恒为0；所有节点都属于不同的社团，模块度恒为负。给定网络的模块度最大称为这个网络的最优分割，对应的模块度记为$Q_{max}$且有$0\leq{Q_{max}}<1$注意到规模较大的网络其对应的Q值也一般较大，因此不能通过模块度的大小比较不同规模网络的社团划分质量。 ### 4.3.3 加权和有向网络的模块度 加权网络的模块度仅需将边数用权值，节点度用节点强度表示即可
$Q_w=\frac1{2W}\sum_{ij}(w_{ij}-\frac{s_is_j}{2W})\delta(C_i,C_j)=\sum_{c=1}^{n_e}{[\frac{W_c}{W}-(\frac{S_e}{2W})^2]}$(4-27)

其中，W是网络中所有边的权值之和，$s_i$是节点i的强度，即与节点i相连的所有边的权值之和，$\omega_{ij}$是点i和j之间边的权值，$\frac{s_is_j}{(2W)}$是相应的零模型中节点i与节点j之间的连边的期望的权值，$W_c$是社团C内部所有边的权重和，$S_c$是所有与社团C内部点相关联的边的权重和。

该公式推广到有向网络有

$Q_d=\frac1M\sum_{ij}(a_{ij}-\frac{k_i^{out}k_j^{in}}{M})\delta(C_i,C_j)$

4.4 基于模块度的社团检测算法

4.4.1 CNM算法

模块度的最大值求解已经被证明是NP难题，因此出现了基于谱优化、模拟退火和极值优化等的近似算法。本节介绍了一种基于贪婪算法思想的凝聚类型的社团结构检测算法CNM算法（Clauset，Newman和Morre提出）。算法的时间复杂度为$O(nlog^2n)$，算法采用堆数据结构计算和更新模块度，具体描述如下：

（1）初始化：初始时假设每个节点就是一个独立的社团，模块度值Q=0，初始的$e_{ij}、a_i$计算如下：

$e_{ij}=\begin{equation}\left\{ \begin{array}{**lr**} {\frac{1}{2M}, 如果i与j间有连边 } &\\ 0,其他\end{array}\right.\end{equation}$ $a_i=\frac{k_i}{2M}$

初始的模块度增量矩阵的元素计算如下：

$\Delta{Q_{ij}}=\begin{equation}\left\{\begin{array}{**lr**}e_{ij}-a_ia_j,\quad\quad如果节点i和j相连 &\\0,\quad其他\end{array}\right.\end{equation}$

得到初始的模块度增量矩阵后，就可以得到由它每一行的最大元素构成的最大堆H

（2）从最大堆H中选择最大的$\Delta{Q}_{ij}$并合并相应的社团i和j，标记合并后的社团为j；并更新模块度增量矩阵$\Delta{Q}_{ij}$、最大堆H和辅助向量$a_j$;

$1.\Delta{Q_{ij}}$的更新：删除第i行和第i列，更新第j行和第j列的元素得到

$\Delta{Q}^{'}_{jk}=\begin{equation}\left\{\begin{array}{**lr**}\Delta{Q_{ik}}+\Delta{Q}_{jk},\quad社团k和社团i和社团j都相连&\\ \Delta{Q}_{ik}-2a_ja_k,\quad 社团k仅与社团i相连，不与社团j相连 &\\ \Delta{Q}_{jk}-2a_ia_k,\quad 社团k仅与社团j相连，不与社团i相连\end{array}\right.\end{equation}$
2.最大堆H的更新：更行最大堆中相应的行和列的最大元素 3.辅助向量$a_i$的更新
$a'_j=a_i+a_j,\quad a'_i=0$

（3）重复步骤2直到网络中所有节点都被划分到一个社团内

4.4.2 层次化社团检测

大规模实际网络中的节点往往具有不同的层次组织结构，大社团内部含有较小的社团。Blondel等人基于模块度概念提出了一种用于加权网络的层次化社团结构分析的凝聚算法BGLL算法，算法分为两个阶段：

初始时假设网络中每个节点都是一个独立的社团。对于任意相邻的节点i和节点j，计算将节点i加入其邻居节点所在的社团的模块度增量$\Delta{Q}:$

$\Delta{Q}=[\frac{W_c+s_{i,in}}{2W}-(\frac{S_c+s_i}{2W})^2]-[\frac{W_c}{2W}-(\frac{S_c}{2W})^2-(\frac{s_i}{2W})^2]$

其中$s_{i,in}$是节点i与社团C内其他节点所有连边的权重和。

构造一个新网络，其中的节点是前一阶段划分的社团，节点之间连边的权重是两个社团之间所有连边的权重和。然后利用之前的方法对于新网络进行社团划分，直到不能划分出更高一层的社团结构为止。

4.5 其他社团检测算法

4.5.1 模块度的局限性

模块度的局限性在于随机的网络都具有正的$Q_{max}$，倘若给定一个划分的模块度为正的，如何判断其是否真正具有较强的社团结构？

一种方法是将给定网络和其一组相应的随机化模型作比较。通常是通过随机重连的方式申城许多具有相同度序列的随机化网络，并计算它们的模块度的均值和方差，分别记为$\langle{Q}\rangle_{NM}$和$\delta_{Q}^{NM}$。然后计算给定网络的统计重要性（中心化）：

$z_Q=\frac{Q_{max}-\langle{Q}\rangle_{NM}}{\delta_Q^{NM}}\quad\quad(4-34)$

如果$z_Q>0$，那么就可以认为网络具有社团结构，并且$z_Q$值越大就表明网络的社团结构越强。这一方法的问题仍在于对$Q_{max}$指标的质疑[1]，一些具有大$Q_{max}$的网络或许并不具有公认的社团结构

模块度的另一个更为重要的问题是分辨率的限制：其无法识别出规模充分小的社团。

4.5.2 派系分割算法

之前介绍的凝聚算法，节点只能被分配到一个社团中，在大型网络中一个节点可能同时属于许多个社团 ，这样的节点称为骑墙节点（Overlapping nodes）。Palla等仍提出了一种派系过滤（Clique percolation）算法来分析具有重叠性的社团结构

1.k-派系社团的定义

k-派系（k-clique）是网络中包含k个节点的全耦合子图，即这k个节点中的任意两个节点之间都有边相连。如果两个k-派系具有k-1个公共节点，那么这两个k-派系是相邻的，如果一个k-派系可以通过若干个相邻的k-派系到达，那么就称这两个派系是连通的。网络中所有彼此连通的k派系就称为一个k-派系社团。例如，网络中的3-派系社团即代表彼此连通的三角形组合，其中任意相邻的两个三角形都具有一条公共边。

如果某个节点属于多个不相邻的k-派系，那么该节点就会位于不同的k-派系社团的重叠部分。下图显示的是4-派系社团，其中浅色的社团与半浅色的社团和神色的社团分别有3个节点和1个节点是重叠的。

2.寻找网络中的派系

在派系过滤算法中，采用由大到小、迭代回归的算法来寻找网络中的派系。首先，从网络中各个节点的度可以判断网络中可能存在的最大全耦合子图的大小s。从网络中一个节点出发，找到所有包含该节点的大小为s的派系后删除该节点以及与之相连的边（以免多次找到同一个派系）。然后，另选一个节点，重复上述步骤，直到网络中没有节点为止。至此找到了网络中大小为s的所有派系。接着逐渐减小s(每次s减小1)，再用上述方法便可寻找到网络中所有大小不同的派系。

这里关键在于如何从一个节点v出发寻找包含它的所有大小为s的派系。为此，首先定义两个集合A和B：集合A为包括节点v在内的两两相连的所有节点的集合，而集合B则为与集合A中各节点都相连的节点的集合，为了避免重复选到某个节点，对集合A和B中的节点都按节点的序号顺序排列。

寻找包含节点v的所有大小为s的派系的迭代回归算法如下：
1.初始集合A={v}，B={v的邻居}；
2.从集合B中移动一个节点到集合A，同时删除集合B中不再与集合A中所有节点相连的节点；
3.如果在集合A的大小未达到s之前，集合B已为空集，或者集合A和B为已有的一个较大派系中地子集，则停止计算，返回上一部。否则，当集合A地大小达到s，就得到一个新的派系，记录该派系，然后发回上一步，继续寻找包含节点v的新的派系。

利用派系寻找k-派系社团

找到网络中的派系以后，可得到派系的重叠矩阵，该矩阵也是对称阵，对角线上的元素对应派系的大小 。在该矩阵中将对角线上值小于k，非对角线上元素小于k-1的元素置为0，其他元素置为1，就可得到k-派系社团的邻接矩阵。各个连通的部分为k派系社团。

实际网络中的情形

实际网络中，规模较大的网络往往在内部节点产生动态变化时较为稳定，而小规模网络则要保证内部节点的相对稳定才可。

4.5.3 连边社团检测算法

2010年Ahn、Bagrow、Lehmann提出了检测具有层次性和层叠性网络的新结构：社团是边的集合而非节点的集合。这样定义的好处在于：尽管一个节点可以属于多个组织，但一条边通常对应明确的含义从而只能属于一个社团。在网络的树图表示中，如果每一个叶子对应一个节点，那么就无法用单个树完整的表示网络的层次结构，而如果用树图的每一个叶子表示一条边，就可以把相应的分支作为社团。在连边树中，由于每条边的节点是的位置是唯一确定的，从而只能属于一个社团。而由于一个节点可以与多条边相连，如果这条边属于不同的社团那么这个节点也相应地属于不同的社团，从而有效地解决重叠节点的问题。此外，通过不同的阈值分割树图可以得到层次化的连边社团结构。

连边社团检测算法的基本操作步骤就是把具有一定相似度的连边合并为一个社团。为此需要给吃连边相似度的定量刻画。假设我们把网络中的每一条边都单独视为一个社团，现在就要把其中两条边合并成一个社团，一个自然的要求就是这两条边有一个公共节点。具有一个公共节点k的一对连边$e_{ik}、e_{jk}$之间相似度的合理定义就是考虑节点对i和j的相似度。第五章将介绍节点对之间相似性的刻画方法。定义连边的相似度如下：

$S(e_{ik},e_{jk})=\frac{|n_+(i)\cup{n_{+}(j)}|}{|n_+(i)\cap{n_+(j)}|}\quad\quad (4-35)$
其中$n_+(i)$为节点i及其所有邻居节点的集合。 利用连边相似度定义，就可以使用分级聚类方法来检测网络社团结构。具体步骤如下： > (1) 计算网络中所有连边对（即至少拥有一个共同节点地连边对）的相似度，并根据相似度的值按降序排列这些连边对。 > (2) 按排列次序依次将连边对所属社团进行合并，将合并过程以以树图的形式记录下来。这里，如果一些连边对具有相同的相似度，那么就在同一步骤合并。 > (3) 社团的合并过程可进行到某一步为止 为了得到最佳的社团结构，需要确定分割树图地最佳位置，或者等价地，确定社团合并过程进行到哪一步是最佳的。为此，基于社团内部的连边密度定义一个目标函数，称为**划分密度(Partition density)D**。假设一个包含M条连边的网络被划分为C个社团{P1,P2,.....,Pc}，其中社团Pc包含mc条连边和nc个节点，它所对应的网络的划分密度就定义为
$D_c=\frac{m_c-(n_c-1)}{n_c(n_c-1)/2-(n_c-1)}\quad\quad(4-36)$
其中$n_c-1$是使得$n_c$个节点构成连通图所需要的最少的边数，而$n_c(n_c-1)/2$是节点间可能存在的最大的边数。这里如果$n_c=2$，那么这个网络的划分密度就定义为0（$D_c=0$）。整个网络的划分密度就定义为$D_c$的加权和：
$D=\frac{1}{M}\sum_cm_cD_c=\frac{2}{M}\sum_{c}m_c\frac{m_c-(n_c-1)}{(n_c-2)(n_c-1)}\quad\quad(4-37)$
由于上式求和中的每一项都局限在社团内部，从而使得划分密度避免块度具有分辨率限制的问题。通过计算连边树图每一层所对应的划分密度或者直接优化划分密度就可以得到最佳的社团划分。注意到D的最大值是1，此时所有的社团都是全耦合关系。另一方面，如果每一个社团都是一棵树（边数最少的连通子图）。那么D等于0，理论上来讲D是有可能是负值的，其下届为-2/3，这是由于两条不相连的边组成的社团所对应的Dc=-2/3,当然在连边社团算法中不会出现这一情形。 采用连边树图的另外一个好处是，不仅在对应于最大划分密度的最优分割处，而且在树图的其他分割线也能得到有意义的社团结构，从而揭示出网络的层次化社团结构特征。 将连边地社团分布转化为节点地社团分布就能找出那些骑墙节点。即使两个节点同时属于不同的社团也能后识别出这条边地多重含义，尽管在连边的社团划分时一条边只能属于一个社团。 ### 4.5.4 #### 1.基准图法 社团检测算法的好坏取决于能否在可接受的范围内给出划分结果和算法能否高质量的实际网络的社团结构，一个方法是人为的构造出一个基准图，基准图的代表是Zachary 空手道俱乐部网络（Zachary's karate club network）。这样一个网络需要具备很多特殊的情况，空手道网络的问题在于其规模太小。 近年来也有一些人工构造出来的网络，例如预设l-划分模型（Planted l-partition model）构造如下： > 网络包含N=g **·** l个节点 ，分为l组，每组包含g个节点。同组的任意两个节点之间的连接概率均为$p_{in}$,不同组的任意两个节点之间的连接概率均为$p_{out}$。这意味着与每组对应的子图是一个ER随机图（详见第7章）。网络节点的平均度为 >
$\langle{k}\rangle=p_{in}(g-1)+p_{out}g(l-1)$
> 如果$p_{in}-p_{out}>0$，意味着每组内部节点之间的连边对更加稠密而不同组之间的连边相对稀疏，从而说明网络具有社团结构；而$p_{in}-p_{out}$值越大，网络社团结构就越明显。常用的一组参数为$l=4,g=32,\langle{k}\rangle=16$从而N=128，$p_{in}+3p_{out}\approx0.5$。在具体计算中，通常使用节点的组内平均度和组外平均度这两个参数 >
$z_{in}=p_{in}(g-1)=31p_{in},\quad z_{out}=p_{out}g(l-1)=96p_{out}$

基准图的问题在于其和实际网络的差异，基准图中的节点度分布是均匀的

2. 元数据方法

举例：一方面如果两个商品被同时购买，那么这两件商品间就有一条边，此外网站上通常会提出商品所属的分类以及用户对其添加的标签等信息，这些信息就被称为元数据。
为了定量比较不同社团划分算法的效果，可以引入以下几个指标：

  1. 社团质量（Community quality）。相似的阶段间应该共享尽可能多的元数据。节点对相似性的富裕度（Enrichment）定义为

    $\frac{\langle{\mu(i,j)}\rangle_{同一社团中所有的i,j}}{\langle{\mu(i,j)\rangle}_{网络中的所有节点对i,j}}$

    其中$\mu(i,j)$是基于元数据的节点i和节点j之间的相似度，对于不同的网络可以有不同的定义。富裕度是位于一个社团中的所有节点对之间的平均元数据相似度，富裕度越大说明社团越紧密。

  2. 重叠质量（Overlap quality）对于网络中每一个节点i我们提取一个标量（称为重叠元数据），它对应于节点i所属的真实社团的的数目。例如，在单词关联网络中，每个社团对应于一组拥有相同话题的单词。一个单词拥有的定义越多，我们期望这个单词属于的话题也越多。因此可以根据某个社团划分算法得到的节点所属的社团数目和该节点的元数据中的重叠信息之间的交互信息（Mutual information）来衡量重叠质量。

  3. 社团覆盖（Community coverage）。计算属于非平凡社团（即有3个或以上节点的社团）的节点所占的比例

  4. 重叠覆盖（Overlap coverage）。计算每个节点所属的非平凡社团的数目的平均值。两个算法可能具有相同的社团覆盖，但是一个算法有可能比另一个算法提取出更多的重叠节点。对于不具有检测重叠性的社团算法，重叠覆盖度与社团覆盖度是一样的。

对上述指标的取值归一化，归一化的值之和就是算法的复合性能（Composite performance）

社团划分的算法还有块模型（Block models）和矩阵分解方法。这两类算法不仅可以用于社团检测，也可用于链路预测（Link prediction）和网络坐标系统（Network coordinate system）等，从而揭示出看似不同问题之间的内在联系