java-lock
Java 锁机制
背景知识
指令流水线
CPU的基本工作是知性存储的指令序列。程序的执行过程实际上是不断地取出指令、分析指令、执行指令的过程。
几乎所有的冯·诺伊曼型计算机的CPU,其工作都可以分为5个阶段:取指令、指令译码、指令执行、访存取数和结果写回。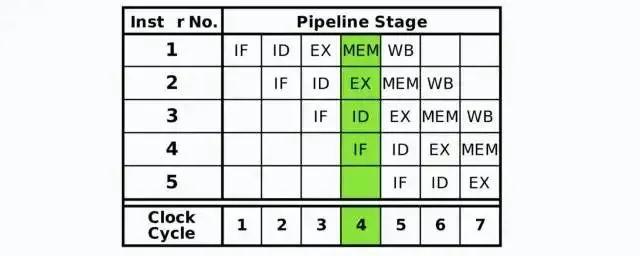
现代处理器的体系结构中,采用了流水线的处理方式对指令进行处理。指令包含了很多阶段,对其进行拆解,每个阶段由专门的硬件电路、寄存器来处理,就可以实现流水线处理。实现更高的CPU吞吐量,但是由于流水线本身的额外开销,可能会增加延迟。
CPU多级缓存
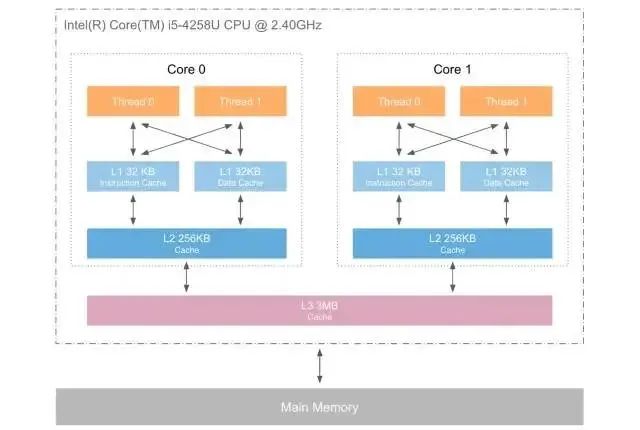
在计算机系统中,CUP高速缓存(CPU Cache,简称缓存)是用于减少处理器访问内存所需平均时间的部件。在金字塔式存储体系中它位于自顶向下的第二层,仅次于CPU寄存器。其容量远小于内存,但速度却可以接近处理器的频率。
当处理器发出内存访问请求时,会先查看缓存内是否由请求数据。如果存在(缓存命中),则不经过访问内存直接返回该数据;如果不存在(缓存失效),则先要把内存当中的数据读到缓存当中,再将其返回处理器。
缓存之所以有限,主要是由于程序运行时对内存的访问呈现局限性的特征(Locality)特征。这种局部性既包括空间局部性(Space Locality),也包括时间局部性(Temporal Locality)。有效利用这种局部性,缓存可以达到极高的命中率。
linux 常用命令
网络科学导论(四)
4 度相关性与社团结构
4.1 引言
度分布并不能唯一的刻画一个网络,因为具有相同度分布的两个网络可能具有风场不同的其他性质或行为。为了进一步刻画网络的拓扑结构我们需要考虑更多结构信息的高阶拓扑性质。本章介绍刻画网络的二阶度分布特性(也称度相关性)几种不同的方法。
即使是联合概率分布也仍然不能完全刻画网络拓扑。一个典型例子就是复杂网络的社团结构:实际网络往往可以看作是由几个社团组成,社团内部的联系较为紧密,而社团间的联系却比较松散。
4.2 度相关性和同配性
4.2.1 高阶度分布的引入
平均度<k>=2M/N可以看作是网络的0阶度分布特性,他除了告诉我们有多少条边之外并没有告诉我们这些边在网络中的任何信息。
网络的度分布P(k)=n(k)/N可以看作是网络的1阶度分布特征<k>=$\sum_{k=0}^\infty{k}P(k)$,具有相同度分布的两个网络有可能具有非常不同的其他性质或是行为。
4.2.2 联合概率分布
联合概率P(j,k)定义为网络中随机选取的一条边的两个端点的度为j和i的概率,即为网络中度为j和度为i的节点之间存在边占网络中总边数的比例:
$P(i,j)=\frac{m(j,k)\mu{(j,k)}}{2M}$
其中,m(i,j)是度为i和度为j的节点之间的边数;如果i=j那么$\mu(i,j)=2$否则为1
网络科学导论(三)
3.1 引言
复杂网络的具体问题在本章才开始进行介绍,包括网络的拓扑性质分析,网络的拓扑建模、网络的行为动力学分析与控制。书中指出,虽然网络科学看起来在基础部分和图论近乎完全一致,但是由于目前复杂网络的规模不是之前理论分析所能达到的,两者在研究方法和研究角度上都有着巨大的不同。较小规模的图可以通过图示的方法。出网络的性质,但对于大规模的网络的研究必须借助强大的计算能力和统计方法。现代网络科学更为关注网络拓扑结构的演变和网上动力学行为之间的关系。
网络规模尺度上的巨大差异使得图论和复杂网络在一些问题上的表述有所不同,经常如果去除某个点使得一个连通片分割为两个连通片那么称该点为割点,而在大规模网络中,去除单个的点和边往往难以对图的连通性产生什么影响,我们往往讨论去除多少比例的节点或边才能将网络分为不同的连通片,对网络的某个性质产生影响
近年来,人们在刻画复杂网络结构的统计特性上提出了许多概念和方法,并且利用了统计物理中的许多方法,包括相变和渗流理论、平均场理论、主方程方法等。
You Are What You Write ver 1.0
写在译前
这篇文章You are what you write是我在2018年寒假时期在知乎上轮子哥的想法分享上看到的,原文大体上不难理解,但是逐字逐句仔细翻译和体会还是需要一定功夫的,之后网上出现不少的翻译结果,但是总感觉对部分的措辞并不认同。现参考谷歌和自己的理解给出自己的版本。在此特别感谢我的表姐,在某些部分的翻译给出自己的建议。